- Appendices
- Slots Analysis
- Miscellaneous
Introduction
Calculate Probability Of Slot Machines
From time to time I get asked specifically how to calculate the return for a slot machine. To avoid breaking any copyright laws I won't use any actual machine as an example but create me own. Lets assume this is a standard three reel electro-mechanical slot machine with the following payoff table based on the center line:
Slot Machine
Suppose you start with $100 and bet a dollar at a time, for example. After inserting all $100 into the slot, 100 pulls later you’ll end up on average with $90, because you lose 10 percent of your money. If you run the $90 back through the machine, you’ll end up with 90 percent of it back, which is 0.90 x 90 = $81. Slot machines are a very popular form of gambling in North America. For example, Ontario, Canada, has approximately 23,000 slot machines, which in the fiscal year 2002- 2003 generated approximately three billion dollars 'after prizes/winnings but before. Winning, are contained in the manufacturers’ design documents, called probability.
| Center Payline | Pays |
|---|---|
Three bars | 5000 |
Three cherries | 1000 |
Three plums | 200 |
Three watermelons | 100 |
Three oranges | 50 |
Three lemons | 25 |
Any two cherries | 10 |
Any one cherry | 2 |
There seems to be always 22 actual stops on each reel of a slot machine. The following table shows the symbol on each stop as well as the weight.
Weight Table
| Symbol | Reel 1 | Reel 2 | Reel 3 |
|---|---|---|---|
Cherry | 3 | 2 | 1 |
Blank | 2 | 3 | 3 |
Plum | 3 | 2 | 2 |
Blank | 2 | 3 | 3 |
Watermelon | 3 | 3 | 2 |
Blank | 2 | 3 | 3 |
Orange | 4 | 3 | 3 |
Blank | 2 | 3 | 3 |
Lemon | 4 | 3 | 3 |
Blank | 5 | 5 | 8 |
Bar | 4 | 3 | 1 |
Blank | 5 | 5 | 7 |
Cherry | 2 | 2 | 1 |
Blank | 2 | 3 | 3 |
Plum | 3 | 2 | 1 |
Blank | 2 | 3 | 3 |
Watermelon | 3 | 2 | 2 |
Blank | 2 | 3 | 3 |
Orange | 3 | 2 | 3 |
Blank | 2 | 3 | 3 |
Lemon | 4 | 3 | 3 |
Blank | 2 | 3 | 3 |
Total | 64 | 64 | 64 |
There are two interesting things to note at this point.First notice that the first reel is weight the most generously and the third is the least. For example the bar has 4 weights on reel 1 and only 1 weight on reel 3. Second notice the high number of blanks directly above and below the bar symbol. This results in a near miss effect.
Most of the symbols occur twice on the reel, and the blank 11 times. The following table shows the total number of weights of each kind of symbol.

Total Weight Table
| Symbol | Reel 1 | Reel 2 | Reel 3 |
|---|---|---|---|
Bar | 4 | 3 | 1 |
Cherry | 5 | 4 | 2 |
Plum | 6 | 4 | 3 |
Watermelon | 6 | 5 | 4 |
Orange | 7 | 5 | 6 |
Lemon | 8 | 6 | 6 |
Blank | 28 | 37 | 42 |
Total | 64 | 64 | 64 |
Given the two table of weights and the pay table it only takes simple math to calculate the expected return. Following are the specific probabilities of each paying combination. Note that each virtual reel has a total of 64 stops so the total number of possible combinations is 643 = 262,144.
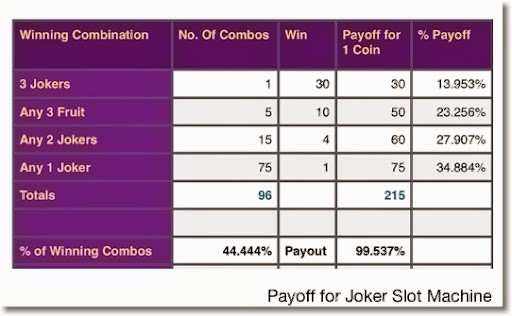
- 3 Bars: 4*3*1/262,144 = 0.000046
- 3 Cherries: 5*4*2/262,144 = 0.000153
- 3 Plums: 6*4*3/262,144 = 0.000275
- 3 Watermelons: 6*5*4/262,144 = 0.000458
- 3 Oranges: 7*5*6/262,144 = 0.000801
- 3 Lemons: 8*6*6/262,144 = 0.001099
- 2 Cherries: (5*4*62 + 5*60*2 + 59*4*2)/262,144 =0.008820
- 1 Cherry: (5*60*62 + 59*4*62 + 59*60*2)/262,144 =0.153778
The average return of the machine is the dot product of the above probabilities and their respective payoffs:
0.000046*5000 + 0.000153*1000 + 0.000275*200 +0.000458*100 + 0.000801*50 + 0.001099*25 + 0.008820*10 +0.153778*2 = 0.94545 .

Thus for every unit played the machine will return back 94.545%.
Go black to slot machines.
Formula For Calculating Probability
Written by: Michael ShacklefordProbability and Data Collection > The Probability of Slot Machines
|